Multihead Latent Attention (MLA)是Deepseek提出的一种新的attention机制,用于减少推理时的内存瓶颈,同时兼顾性能提升和缓存效率。本文将对MLA的原理、实现和效果进行解读。
Notations
| Symbol | Description |
|---|---|
| $d_h$ | dimension of embedding per attention head |
| $d_c$ | the KV compression dimension in MLA |
| $d_r^R$ | the per-head dimension of the decoupled queries and key in MLA |
| $n_h$ | number of attention heads |
| $l$ | the transformer layer number |
| $h_t \in \mathbb{R}^{d}$ | the attention input of $t$-th token at an attention layer |
| $u_t \in \mathbb{R}^{d}$ | the output hidden of $t$-th token at an attention layer |
背景
auto-regressive的LLM主要是decoder的架构,基于先前生成的tokens来预测下一个token。生成过程是顺序的,会用到历史token的KV来保证生成的连贯性,直到最大长度或者生成结束符。 每一步的output作为下次input时,需要进行tokenlizer、embedding、MLP投影生成Q,K,V,这时为了避免重复计算,会将KV做cache;但是在常用MHA中,kVcache的大小会随着token长度的增加而增加,导致内存瓶颈。
回顾下MHA的计算公式更清楚KV cache线性增长的现状:
$$ [q_{t, 1};q_{t, 2};…;q_{t, n_h}] = W_qh_t$$ $$ [k_{t, 1};k_{t, 2};…;k_{t, n_h}] = W_kh_t$$ $$ [v_{t, 1};v_{t, 2};…;v_{t, n_h}] = W_vh_t$$
其中$W_q, W_k, W_v$是权重矩阵,$h_t$是输入的embedding,$q_{t, i}, k_{t, i}, v_{t, i}$是第$t$个token第$i$个head的QKV。
针对每个head,计算attention score,然后加权求和得到output:
$$ o_{t, i} = \sum_{j=1}^{t} Softmax_j(\frac{q_{t, i}k_{j, i}^T}{\sqrt{d_h}})v_{j, i}$$ $$ u_t = W^o[o_{t, 1};o_{t, 2};…;o_{t, n_h}]$$
其中$W^o$是每个head拼接后用于最终输出的投影权重矩阵,$o_{t, i}$是第$t$个token第$i$个head的output。
在MLA提出之前,为减少KV cache,已经有GQA和MQA等方法。 Multi-Query Attention (MQA): 所有Attention Head共享同一组KV,极大减少了KV cache的大小,但是性能有所下降。 Grouped-Query Attention (GQA): 将Attention Head分组,每组共享同一组KV,减少KV cache的大小,是MHA和MQA的折中方案。
具体思想对比可以看下图:
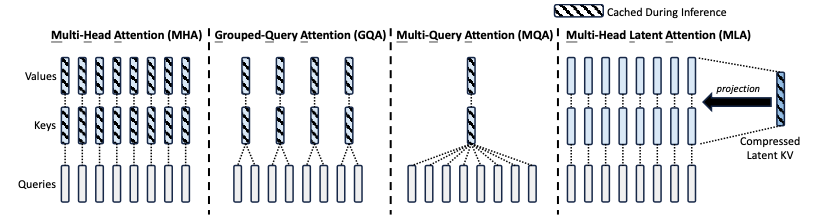
MLA具体实现
MLA的核心思想是通过low-rank joint compression 来共享KV,减少cache大小,同时保持性能。
低秩压缩
具体来说,MLA的计算公式如下:
$$ {c^{KV}_t} = W^{DKV}h_t$$ $$ k^C_t = W^{UK}c^{KV}_t$$ $$ v^C_t = W^{UV}c^{KV}_t$$
其中$c^{KV}_t$是compressed的KV,推理阶段被用来存储到KV cache,对应维度为$d_c$,该维度远远小于$d_hn_h$。 $W^{DKV}\in \mathbb{R}^{d_c \times d_hn_h}$是压缩权重矩阵。 $W^{UK}, W^{UV}$是KV分别的上投影权重矩阵。推理时,$W^{UK}$可以合并到$W^Q$,$W^{UV}$可以合并到$W^O$。
另外,为了减少训练过程中的内存占用,MLA还对Query也进行低秩压缩,方法跟KV的一样,公式如下:
$$ c^{Q}_t = W^{DQ}h_t$$ $$ q^C_t = W^{UQ}c^{Q}_t$$
其中,$c^{Q}_t$是compressed的$Q$,对应维度为$d_c’$,$W^{DQ}\in \mathbb{R}^{d_c’ \times d_h}$是压缩权重矩阵,$W^{UQ} \in \mathbb{R}^{d_nn_h \times d_c’}$是Q的上投影权重矩阵。
Decoupled Rotary Position Embedding
RoPE是一种旋转位置编码,通过旋转操作改变每个token的表示,使得模型能同时感知绝对位置和相对位置。
因为MLA中的KV是压缩的,直接使用RoPE会导致位置编码信息丢失。具来说,标准RoPE中,Query和Key都会应用RoPE,但是在MLA中,Key是压缩的,并且当前token对应的K的RoPE matrix,会被放在 $W^Q$ 和 $W^{UK}$ 中,RoPE 矩阵的插入会影响乘法的顺序和结构。
所以这里的decoupled是指Q和K分别使用不同的RoPE。先看公式:
$$ [q^C_{t, 1};…;q^C_{t, n_h}]=RoPE(W^{QR}c^Q_t)$$ RoPE之后,每个head都会拆分出对应的RoPE $$ q_{t,i}=[q^C_{t, i};q^R_{t, i}]$$ 用于计算attention score 的Q是拼接了RoPE的Q $$ {k^R_t} = RoPE(W^{KR}h_t)$$ 这个是所有$K$共享的位置编码,会存到cache中 $$ k{t,i}=[k^C_{t, i};k^R_t]$$
那么最后的attention score计算就变成了:
$$ o_{t, i} = \sum_{j=1}^{t} Softmax_j(\frac{q_{t, i}k_{j, i}^T}{\sqrt{d_h+d^R_h}})v^C_{j, i}$$
这个时候,再来看这张图就很清晰了:
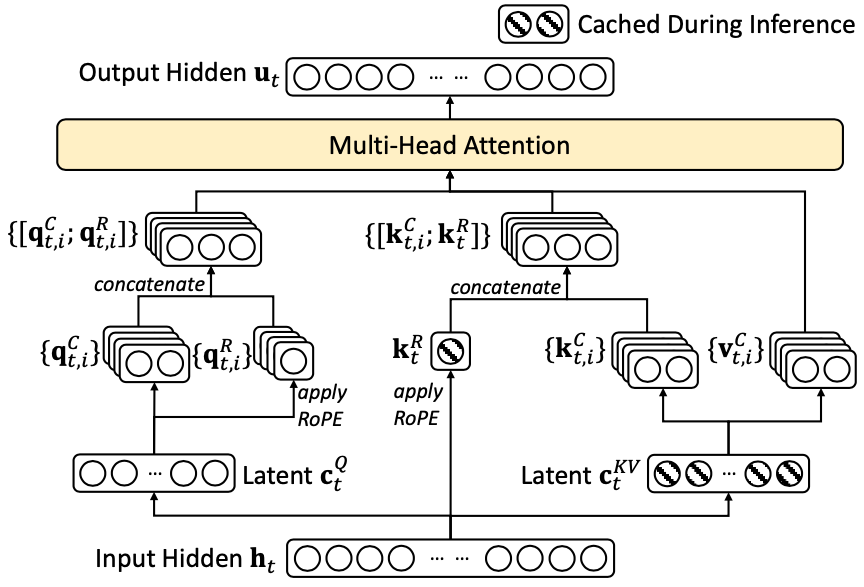
效果
| method | KV cache per Token | capability |
|---|---|---|
| MHA | $2n_h \times d_h \times l$ | Strong |
| GQA | $2n_g \times d_h \times l$ | Moderate |
| MQA | $2d_h \times l$ | Weak |
| MLA | $(d_c + d_r^R) \times l \approx \frac{9}{2}d_hl$ | Stronger |
在deepseek的实现中,$n_c=4d_h$, $d_r^R=\frac{d_h}{2}$
在benchmark上的对比结果:
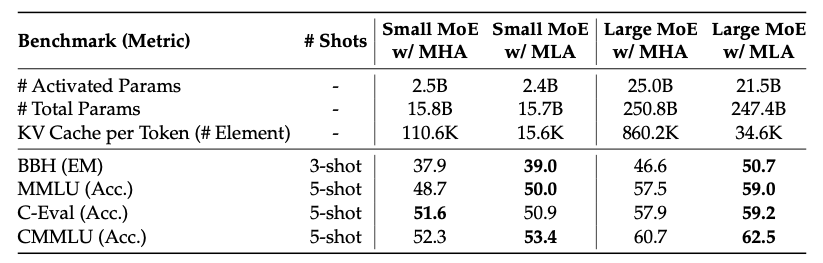
为什么MLA的性能对齐并超过MHA?
一般的LLM架构参数满足num_heads * head_size = hidden_size,但DeepSeek不一样,head数量是一般设置的3倍。这是因为MLA的KV Cache大小跟num_heads无关,增大num_heads只会增加计算量和提升模型能力,但不会增加KV Cache,所以不会带来速度瓶颈。